حركة توافقية بسيطة


الحركة التوافيقة البسيطة: هي حركة إهتزازية في خط مستقيم يتناسب فيها تسارع الكتلة طرديا مع مقدار الإزاحة، ويعاكسها في الإتجاه، أو الحركة التي تكرر نفسها كل فترة زمنية، وتكون سعة اهتزاز الحركة ثابتة، تتناسب العجلة مع إزاحة الجسم من موضع الإتزان ويكون اتجاهها دائما إلى موضع الإتزان. ومن الأمثلة عليها:
وتوصف هذه الحركة بسعة الاهتزاز (وهي موجبة دائما) والزمن الدوري (الزمن الذي يستغرقه الجسم لعمل أهتزازة كاملة) والتردد (عدد الأهتزازات في الثانية الواحدة) وأخيرا الطور الذي يحدد مكان بدأ الحركة على منحنى ال Sine، ويكون كل من التردد والزمن الدوري ثابتان اما سعة الاهتزاز والطور فيتم تحديدهما عن طريق الشروط الابتدائية للحركة.
المعادلة العامة التي تصف الحركة التوافقية البسيطة هي حيث x يمثل الأزاحة وA هو سعة الاهتزاز وf هو التردد وt الزمن و
حيث x يمثل الأزاحة وA هو سعة الاهتزاز وf هو التردد وt الزمن و هو الطور. عند انعدام الإزاحة عند بداية الحركة عند t = 0 فإن الطور يساوي
هو الطور. عند انعدام الإزاحة عند بداية الحركة عند t = 0 فإن الطور يساوي 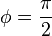 .
.

حركة توافقية بسيطة (جسيم متأثر بموجة بحر).
4 العلاقة بين الحركة الدائرية والتوافقية البسيطة
4.1 السرعة الزاوية
5 معادلات الحركة التوافقية البسيطة
5.1 السرعة في الحركة التوافقية البسيطة
6 الطاقة في الحركة التوافقية البسيطة
7 انظر أيضا
8 مصادر

حركة توافقية بسيطة (كتلة على زنبرك وحركة على دائرة)
من أفضل الأمثلة للحركة التوافقية البسيطة هو الكتلة المثبتة في زنبرك.
في حالة عدم تمدد الزنبرك لا تؤثر أي قوة على الكتلة المثبتة، أي يكون النظام متزن ومستقر. وعند ابتعاد الكتلة عند موضع الاستقرار أو الأتزان سيقوم الزنبرك ببذل قوة لإعادتهامرة أخرى إلى موضعها الأصلي، وتعطى هذه القوة حسب قانون هوك بالعلاقة : حيث F هي القوة التي يولدها الزنبرك وx الأزاحة وk ثابت الزنبرك.
حيث F هي القوة التي يولدها الزنبرك وx الأزاحة وk ثابت الزنبرك.
عامة أي نظام يتحرك بحركة توافقية بسيطة يحتوي على سمتان رئيسيتان.أولا عند التحرك بعيدا عن مركز الأتزان يتم بذل قوة لإعادة النظام مرة أخرى إلى وضع الأتزان، القوة المبذولة تتناسب طرديا مع الأزاحة التي يقوم بها النظام، والمثال الذي تناولناه (الكتلة المثبتة بالزنبرك)يحقق السمتان.
بالعودة مرة أخرى للمثال، عند تحرك الكتلة بعيدا عن موضع الأتزان يبذل الزنبرك قوة أستعادة حتى يعيدها مرة أخرى إلى وضعها السابق، وكلما أقتربت الكتلة من وضع الأتزان تتناقص قوة الأستعادة تدريجيا لأنها تتناسب مع الأزاحة، لذا فعند موضع الأتزان x=0 تنعدم هذه القوة على الكتلة، ولكن الكتلة تظل محتفظة ببعض من كمية التحرك من الحركة السابقة لذا فهي لا تتوقف عند مركز الأتزان ولكن تتعداه وعندها تظهر قوة الأستعادة مرة أخرى وتقوم بإبطائها تدريجيا حتى تنعدم سرعتها في النهاية وتصل إلى موضع الأتزان في النهاية.
و إذا لم تفقد الكتلة طاقتها ستستمر في الاهتزاز، لذا فهي حركة دورية تتكرر كل فترة زمنية وسنوضح بعد ذلك أنها حركة توافقية بسيطة.
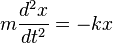 حيث k ثابت موجب القيمة وm كتلة الجسم وx الأزاحة. وباستخدام السرعة الزاوية
حيث k ثابت موجب القيمة وm كتلة الجسم وx الأزاحة. وباستخدام السرعة الزاوية  التي تعرف كالتالي :
التي تعرف كالتالي :

فإن ازاحة الجسم في الحركة التوافقية البسيطة تعرف كالتالي (1):
 (استخدام الدالة Sine أو Cosine لن يحدث فرقا قالناتج النهائي في معادلة 4 سيكون ثابت في الحالتين)
(استخدام الدالة Sine أو Cosine لن يحدث فرقا قالناتج النهائي في معادلة 4 سيكون ثابت في الحالتين)
وبتفاضل العلاقة مرة نحصل على السرعة عند أي زمن (2):

وبتفاضل العلاقة مرتين نحصل على العجلة عند أي زمن (3) :

وبالتعويض بالمعادلة (1) في المعادلة (3) نحصل على علاقة بين العجلة والأزاحة (4) :

والتي تساوي :

كتلة مثبتة في زنبرك - حركة توافقية بسيطة.
هناك العديد من الأمثلة على الحركة التوافقية البسيطة سنتناول البعض منها.

ويمكن إيجاد الزمن الدوري بالعلاقة :
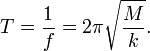
يعتمد الزمن الدوري على كل من سعة الاهتزاز وعجلة الجاذبية الأرضية.
 على دائرة قطرها R حول نقطة الأصل في محاور x-y فإن إسقاط موضع الجسم على محور x ومحور y يمثلان حركة توافقية بسيطة بسعة اهتزاز R وسرعة زاوية
على دائرة قطرها R حول نقطة الأصل في محاور x-y فإن إسقاط موضع الجسم على محور x ومحور y يمثلان حركة توافقية بسيطة بسعة اهتزاز R وسرعة زاوية  .
.

البندول البسيط يتحرك حركة توافقية بسيطة إذا كانت سعة الاهتزاز صغيرة جدا.
يتكون البندول البسيط من كتلة مربوطة بخيط مثبت في حامل أفقي كما في الشكل صورة "البندول البسيط". عند إزاحة الكتلة بزاوية صغيرة (θم) عن الوضع الرأسي و تركها فإنها تتحرك متذبذبة على الجانبين. وتعد حركة البندول البسيط حركة توافقية بسيطة والزمن الدوري للكتلة المثبتة في خيط بندول طوله وعجلة جاذبية أرضية
وعجلة جاذبية أرضية  يعطى بالعلاقة :
يعطى بالعلاقة :
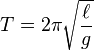
الزمن الدوري يعتمد على كل من سعة الاهتزاز وكتلة البندول. تكون هذه العلاقة دقيقة في حالة الزوايا الصغيرة لأن العجلة الزاوية تتناسب مع جيب الموضع:

حيث I هو عزم القصور الذاتي ويعطى بالعلاقة :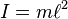 وعندما تكون الزاوية
وعندما تكون الزاوية  صغيرة جدا يكون
صغيرة جدا يكون  فتصبح العلاقة :
فتصبح العلاقة :
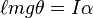
أي ان العجلة الزاوية تتناسب مع (عجلة تتناسب مع أزاحة) وذلك يحقق شرط الحركة التوافقية البسيطة.
(عجلة تتناسب مع أزاحة) وذلك يحقق شرط الحركة التوافقية البسيطة.
عندما تكون الكتلة في أعلى موضع لها عند النطقة (أ)، فإن سرعتها تساوي صفراً و تكون الكتلة تحت تأثير مركبة الوزن (وجاθم) فإنها تعمل على نفس خط قوة الشد في الخيط. و عندما تترك الكتلة فإن الزاوية (θ) تتناقص حتى تصبح صفراً في الوضع الرأسي، ثم تبدأ بالزيادة حتى تصل إلى أكبر قيمة (θم) عند النقطة (ب) في الجهة المقابلة.
و بالتعويض في قانون نيوتن الثاني، نجد أن محصلة القوى في اتجاه الحركةهي:
Σ ق = ك ت، أي أن:
وجاθ = - ك ت
وحيث إن وزن الكتلة و = ك ج، ج= تسارع الجاذبية الأرضية، فإن:
ك جـ جاθ = - ك ت، أي أن:
ت = - جـ جاθ.
و بما أن (θم) زاوية صغيرة (θ < 15)، فإن جاθ = (طول القوس ÷ نصف القطر) ≈ (س ÷ ل)، فإن:
ت = -(جـ ÷ ل) × س ← ت = ∞ - س
لاحظ هنا أن تسارع البندول يتناسب عكسيا مع الإزاحة، أي أن البندول البسيط يتحرك حركة توافقية بسيطة.
إن القوة المؤثرة على الجسم تكون دائماً بإتجاه المركز و لنفرض أن هذه القوى تساوي قم، نحلل هذه القوة إلى مركبتين متعامدتين قص، قس.
من صورة "الحركة الدائرية" يلاحظ أن قص = قم جاθ و إتجاهها إلى الأسفل، و بما أن:
جاθ = ص ÷ س، فإن قص = - قم ص ÷ نق. و بقسمة طرفي هذه المعادلة على الكتلة نحصل على:
تص = -تم = ص ÷ نق = - (تم ÷ نق) × ص، أي أن تسارع الجسم في الإتحاه الصادي يتناسب عكسيا مع الإزاحة، و عليه فإن مسقط حركة الجسم على المحور الصادي هي حركة تواقية بسيطة. و ينطبق الحديث نفسه على مسقط حركة الجسم على المحور السيني، أي أن الحركة في الإتجاه السيني هي أيضاً حركة توافقية يسيطة.
ع = ∆ل ÷ ∆ز = نق ∆θ ÷ ∆ز = نق (∆θ ÷ ∆ز)
تعرف السرعة الزاوية ( ) بأنها مقدار الزاوية التي يقطعها الجسم أثناء الحركة الدائرية في وحدة الزمن، أي أن:
) بأنها مقدار الزاوية التي يقطعها الجسم أثناء الحركة الدائرية في وحدة الزمن، أي أن:
 = ∆θ ÷ ∆ز. و بناء على ذلك فإن السرعة الخطية ع = نق
= ∆θ ÷ ∆ز. و بناء على ذلك فإن السرعة الخطية ع = نق  .
.
ومن المعروف أن التسارع المركزي لجسم في حركة دائرة منتظمة تم = ع2 ÷ نق = (نق )2 ÷ نق = نق
)2 ÷ نق = نق  2. و من خلال ذلك يمكن كتابة معادلة التسارع للحركة التوافقية البسيطة كالتالي:
2. و من خلال ذلك يمكن كتابة معادلة التسارع للحركة التوافقية البسيطة كالتالي:
تص = - (تص ÷ نق) × ص = - 2 ص
2 ص
والسرعة الزاوية تساوي حاصل قسمة الزاوية الكلية التي يقطعها الجسم في دورة كاملة و تساوي (π2) على زمن الدورة (ن)، أي أن:
تساوي حاصل قسمة الزاوية الكلية التي يقطعها الجسم في دورة كاملة و تساوي (π2) على زمن الدورة (ن)، أي أن:  = π2 ÷ ن، و منه د (التردد) = 1 ÷ ن =
= π2 ÷ ن، و منه د (التردد) = 1 ÷ ن =  ÷ π2.
÷ π2.
قيمة الزاوية  تعتمد على:
تعتمد على:
في الصورة "مركبات الحركة الدائرية" يكون الجسم في النقطة (هـ) فإنه يقطع المسافة (ص) على المحور الصادي.
و حيث إن ص = نق جاθ، فإن إزاحة الجسم الذي يتحرك حركة توافقية بسيطة تتغير كدالة جيبية بتغير الزاوية θ كما في الصورة. و بما أن الزاوية θ هي الزاوية التي قطعها الجسم في الزمن (ز) فإن θ = ز، و بشكل عام يمكن كتابة معادلة الإزاحة في الحركة التوافقية البسيطة:
ز، و بشكل عام يمكن كتابة معادلة الإزاحة في الحركة التوافقية البسيطة:
ص(ز) = صم جا( ز + ϕ)
ز + ϕ)
حيث، صم: أقصى إزاحة ممكنة للكتلة عن نقطة الإتزان و تساوي نق. ز: الزمن بوحدة الثانية. ϕ: زاوية ثابط الطور، وتحدد موضع الجسم عندما يكون الزمن يساوي صفراً، و تحسب من معرفة موضع الجسم و سرعته عند لحظة معينة.
لاحظ من الصورة "الإزاحة في الحركة التوافقية البسيطة" أن صم تمثل سعة الإهتزاز، و تساوي البعدين نقطة الإتزان و أبعد نقطة ممكنة للحركة، و أن الزمن الدوري (ن) هو الفترة الزمنية التي تفصل بين مرور الجسم في نقطتين متماثلتين في الطور من حيث:

لاحظ أن جيب الزاوية = جيب تمام الزاوية المتممة
عس = ع جا( ز)، و حيث أن ع =
ز)، و حيث أن ع =  نق، فإن:
نق، فإن:
عس = نق جا(
نق جا( ز)
ز)
و لحساب تسارع الجسم في أي لحظة يتم تعويض المعادلة
تس = - 2 سم جا(
2 سم جا( ز).
ز).
ويسمى مجموع هذين الشكلين من الطاقة بالطاقة الميكانيكية للنظام (طم)؛ أي أن:
طم = طو + طح
طم = (1÷2) أ س2 + (1÷2) ك ع2
وبإهمال قوة الاحتكاك وكتلة النابض يكون مقدار الطاقة الميكانيكية ثابتاً عند جميع النقاط في مسار الجسم.
وفي اللحظة التي يكون فيها الجسم أبعد ما يمكن عن نقطة الاتزان، تكون سرعته تساوي صفراً؛ أي أن:

لاحظ الصورة التي تمثل الطاقة الميكانيكية لكتلة مربوطة في نابض.


الحركة التوافيقة البسيطة: هي حركة إهتزازية في خط مستقيم يتناسب فيها تسارع الكتلة طرديا مع مقدار الإزاحة، ويعاكسها في الإتجاه، أو الحركة التي تكرر نفسها كل فترة زمنية، وتكون سعة اهتزاز الحركة ثابتة، تتناسب العجلة مع إزاحة الجسم من موضع الإتزان ويكون اتجاهها دائما إلى موضع الإتزان. ومن الأمثلة عليها:
وتوصف هذه الحركة بسعة الاهتزاز (وهي موجبة دائما) والزمن الدوري (الزمن الذي يستغرقه الجسم لعمل أهتزازة كاملة) والتردد (عدد الأهتزازات في الثانية الواحدة) وأخيرا الطور الذي يحدد مكان بدأ الحركة على منحنى ال Sine، ويكون كل من التردد والزمن الدوري ثابتان اما سعة الاهتزاز والطور فيتم تحديدهما عن طريق الشروط الابتدائية للحركة.
المعادلة العامة التي تصف الحركة التوافقية البسيطة هي
 حيث x يمثل الأزاحة وA هو سعة الاهتزاز وf هو التردد وt الزمن و
حيث x يمثل الأزاحة وA هو سعة الاهتزاز وf هو التردد وt الزمن و هو الطور. عند انعدام الإزاحة عند بداية الحركة عند t = 0 فإن الطور يساوي
هو الطور. عند انعدام الإزاحة عند بداية الحركة عند t = 0 فإن الطور يساوي 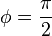 .
.
حركة توافقية بسيطة (جسيم متأثر بموجة بحر).
محتويات
مقدمة

حركة توافقية بسيطة (كتلة على زنبرك وحركة على دائرة)
من أفضل الأمثلة للحركة التوافقية البسيطة هو الكتلة المثبتة في زنبرك.
في حالة عدم تمدد الزنبرك لا تؤثر أي قوة على الكتلة المثبتة، أي يكون النظام متزن ومستقر. وعند ابتعاد الكتلة عند موضع الاستقرار أو الأتزان سيقوم الزنبرك ببذل قوة لإعادتهامرة أخرى إلى موضعها الأصلي، وتعطى هذه القوة حسب قانون هوك بالعلاقة :
 حيث F هي القوة التي يولدها الزنبرك وx الأزاحة وk ثابت الزنبرك.
حيث F هي القوة التي يولدها الزنبرك وx الأزاحة وk ثابت الزنبرك.عامة أي نظام يتحرك بحركة توافقية بسيطة يحتوي على سمتان رئيسيتان.أولا عند التحرك بعيدا عن مركز الأتزان يتم بذل قوة لإعادة النظام مرة أخرى إلى وضع الأتزان، القوة المبذولة تتناسب طرديا مع الأزاحة التي يقوم بها النظام، والمثال الذي تناولناه (الكتلة المثبتة بالزنبرك)يحقق السمتان.
بالعودة مرة أخرى للمثال، عند تحرك الكتلة بعيدا عن موضع الأتزان يبذل الزنبرك قوة أستعادة حتى يعيدها مرة أخرى إلى وضعها السابق، وكلما أقتربت الكتلة من وضع الأتزان تتناقص قوة الأستعادة تدريجيا لأنها تتناسب مع الأزاحة، لذا فعند موضع الأتزان x=0 تنعدم هذه القوة على الكتلة، ولكن الكتلة تظل محتفظة ببعض من كمية التحرك من الحركة السابقة لذا فهي لا تتوقف عند مركز الأتزان ولكن تتعداه وعندها تظهر قوة الأستعادة مرة أخرى وتقوم بإبطائها تدريجيا حتى تنعدم سرعتها في النهاية وتصل إلى موضع الأتزان في النهاية.
و إذا لم تفقد الكتلة طاقتها ستستمر في الاهتزاز، لذا فهي حركة دورية تتكرر كل فترة زمنية وسنوضح بعد ذلك أنها حركة توافقية بسيطة.
رياضيا
تعرف الحركة التوافقية البسيطة بالمعادلة التفاضلية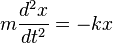 حيث k ثابت موجب القيمة وm كتلة الجسم وx الأزاحة. وباستخدام السرعة الزاوية
حيث k ثابت موجب القيمة وm كتلة الجسم وx الأزاحة. وباستخدام السرعة الزاوية  التي تعرف كالتالي :
التي تعرف كالتالي :
فإن ازاحة الجسم في الحركة التوافقية البسيطة تعرف كالتالي (1):
 (استخدام الدالة Sine أو Cosine لن يحدث فرقا قالناتج النهائي في معادلة 4 سيكون ثابت في الحالتين)
(استخدام الدالة Sine أو Cosine لن يحدث فرقا قالناتج النهائي في معادلة 4 سيكون ثابت في الحالتين)وبتفاضل العلاقة مرة نحصل على السرعة عند أي زمن (2):

وبتفاضل العلاقة مرتين نحصل على العجلة عند أي زمن (3) :

وبالتعويض بالمعادلة (1) في المعادلة (3) نحصل على علاقة بين العجلة والأزاحة (4) :

والتي تساوي :

أمثلة

كتلة مثبتة في زنبرك - حركة توافقية بسيطة.
هناك العديد من الأمثلة على الحركة التوافقية البسيطة سنتناول البعض منها.
كتلة مثبتة في زنبرك
الكتلة (m) المثبتة في زنبرك بثابت (k) تتحرك حركة توافقية بسطية بعجلة زاوية :
ويمكن إيجاد الزمن الدوري بالعلاقة :
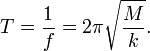
يعتمد الزمن الدوري على كل من سعة الاهتزاز وعجلة الجاذبية الأرضية.
الحركة الدائرية
يمكن اعتبار الحركة التوافقية البسيطة في بعض الأحيان على أنها إسقاط أحادي البعد لحركة دائرية، عند دوران جسم بسرعة زاوية على دائرة قطرها R حول نقطة الأصل في محاور x-y فإن إسقاط موضع الجسم على محور x ومحور y يمثلان حركة توافقية بسيطة بسعة اهتزاز R وسرعة زاوية
على دائرة قطرها R حول نقطة الأصل في محاور x-y فإن إسقاط موضع الجسم على محور x ومحور y يمثلان حركة توافقية بسيطة بسعة اهتزاز R وسرعة زاوية  .
.البندول البسيط
 مقالة مفصلة: بندول (رياضيات)
مقالة مفصلة: بندول (رياضيات)

البندول البسيط يتحرك حركة توافقية بسيطة إذا كانت سعة الاهتزاز صغيرة جدا.
يتكون البندول البسيط من كتلة مربوطة بخيط مثبت في حامل أفقي كما في الشكل صورة "البندول البسيط". عند إزاحة الكتلة بزاوية صغيرة (θم) عن الوضع الرأسي و تركها فإنها تتحرك متذبذبة على الجانبين. وتعد حركة البندول البسيط حركة توافقية بسيطة والزمن الدوري للكتلة المثبتة في خيط بندول طوله
 وعجلة جاذبية أرضية
وعجلة جاذبية أرضية  يعطى بالعلاقة :
يعطى بالعلاقة :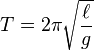
الزمن الدوري يعتمد على كل من سعة الاهتزاز وكتلة البندول. تكون هذه العلاقة دقيقة في حالة الزوايا الصغيرة لأن العجلة الزاوية تتناسب مع جيب الموضع:

حيث I هو عزم القصور الذاتي ويعطى بالعلاقة :
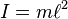 وعندما تكون الزاوية
وعندما تكون الزاوية  صغيرة جدا يكون
صغيرة جدا يكون  فتصبح العلاقة :
فتصبح العلاقة :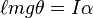
أي ان العجلة الزاوية تتناسب مع
 (عجلة تتناسب مع أزاحة) وذلك يحقق شرط الحركة التوافقية البسيطة.
(عجلة تتناسب مع أزاحة) وذلك يحقق شرط الحركة التوافقية البسيطة.عندما تكون الكتلة في أعلى موضع لها عند النطقة (أ)، فإن سرعتها تساوي صفراً و تكون الكتلة تحت تأثير مركبة الوزن (وجاθم) فإنها تعمل على نفس خط قوة الشد في الخيط. و عندما تترك الكتلة فإن الزاوية (θ) تتناقص حتى تصبح صفراً في الوضع الرأسي، ثم تبدأ بالزيادة حتى تصل إلى أكبر قيمة (θم) عند النقطة (ب) في الجهة المقابلة.
و بالتعويض في قانون نيوتن الثاني، نجد أن محصلة القوى في اتجاه الحركةهي:
Σ ق = ك ت، أي أن:
وجاθ = - ك ت
وحيث إن وزن الكتلة و = ك ج، ج= تسارع الجاذبية الأرضية، فإن:
ك جـ جاθ = - ك ت، أي أن:
ت = - جـ جاθ.
و بما أن (θم) زاوية صغيرة (θ < 15)، فإن جاθ = (طول القوس ÷ نصف القطر) ≈ (س ÷ ل)، فإن:
ت = -(جـ ÷ ل) × س ← ت = ∞ - س
لاحظ هنا أن تسارع البندول يتناسب عكسيا مع الإزاحة، أي أن البندول البسيط يتحرك حركة توافقية بسيطة.
العلاقة بين الحركة الدائرية والتوافقية البسيطة
نفترض أن جسما ما يسير في مسار دائري نصف قطره (نق) و مركزه (م) كما في صورة "الحركة الدائرية"، و أن هذا الجسم بدأ الحركة من النقطة (أ) على محور السينات ماراً بالنقطة (هـ) بعكس اتجاه عقارب الساعة.إن القوة المؤثرة على الجسم تكون دائماً بإتجاه المركز و لنفرض أن هذه القوى تساوي قم، نحلل هذه القوة إلى مركبتين متعامدتين قص، قس.
من صورة "الحركة الدائرية" يلاحظ أن قص = قم جاθ و إتجاهها إلى الأسفل، و بما أن:
جاθ = ص ÷ س، فإن قص = - قم ص ÷ نق. و بقسمة طرفي هذه المعادلة على الكتلة نحصل على:
تص = -تم = ص ÷ نق = - (تم ÷ نق) × ص، أي أن تسارع الجسم في الإتحاه الصادي يتناسب عكسيا مع الإزاحة، و عليه فإن مسقط حركة الجسم على المحور الصادي هي حركة تواقية بسيطة. و ينطبق الحديث نفسه على مسقط حركة الجسم على المحور السيني، أي أن الحركة في الإتجاه السيني هي أيضاً حركة توافقية يسيطة.
السرعة الزاوية
عندما يقطع جسم يسير في حركة دائرية منتظمة زاوية مقدارها ∆θ في زمن مقداره ∆ز، فإنه يقطع قوسا طوله ∆ل، كما يظهر في صورة "سرعة الزاوية". و لحساب مقدار سرعته يتم تقسيم طول القوس على الفترة الزمنية؛ أي أن:ع = ∆ل ÷ ∆ز = نق ∆θ ÷ ∆ز = نق (∆θ ÷ ∆ز)
تعرف السرعة الزاوية (
 ) بأنها مقدار الزاوية التي يقطعها الجسم أثناء الحركة الدائرية في وحدة الزمن، أي أن:
) بأنها مقدار الزاوية التي يقطعها الجسم أثناء الحركة الدائرية في وحدة الزمن، أي أن: = ∆θ ÷ ∆ز. و بناء على ذلك فإن السرعة الخطية ع = نق
= ∆θ ÷ ∆ز. و بناء على ذلك فإن السرعة الخطية ع = نق  .
.ومن المعروف أن التسارع المركزي لجسم في حركة دائرة منتظمة تم = ع2 ÷ نق = (نق
 )2 ÷ نق = نق
)2 ÷ نق = نق  2. و من خلال ذلك يمكن كتابة معادلة التسارع للحركة التوافقية البسيطة كالتالي:
2. و من خلال ذلك يمكن كتابة معادلة التسارع للحركة التوافقية البسيطة كالتالي:تص = - (تص ÷ نق) × ص = -
 2 ص
2 صوالسرعة الزاوية
 تساوي حاصل قسمة الزاوية الكلية التي يقطعها الجسم في دورة كاملة و تساوي (π2) على زمن الدورة (ن)، أي أن:
تساوي حاصل قسمة الزاوية الكلية التي يقطعها الجسم في دورة كاملة و تساوي (π2) على زمن الدورة (ن)، أي أن:  = π2 ÷ ن، و منه د (التردد) = 1 ÷ ن =
= π2 ÷ ن، و منه د (التردد) = 1 ÷ ن =  ÷ π2.
÷ π2.معادلات الحركة التوافقية البسيطة
فكانت نتيجة البند السابق العلاقات التي تربط تسارع الأجسام في الحركة التوافقية البسيطة مع الإزاحة، سواء في النابض أو البندول أو الحركة في مسار دائري منظم، فكانت على النحو الآتي:| في النابض | ت = - (أ ÷ ك) × س | أو | ت = - ( 2 س) 2 س) |
| في البندول | ت = - (ج ÷ ل) × س | أو | ت = - ( 2 س) 2 س) |
| في الحركة الدائرية | ت = س = - تم ÷ نق × س | أو | تس = - ( 2 س) 2 س) |
 تعتمد على:
تعتمد على:- ثابت المرونة وكتلة الجسم في النابض.
- تسارع الجاذبية وطول الخيط في البندول.
- تسارع الجسم ونصف قطر المدار في الحركة الدائرية.
في الصورة "مركبات الحركة الدائرية" يكون الجسم في النقطة (هـ) فإنه يقطع المسافة (ص) على المحور الصادي.
و حيث إن ص = نق جاθ، فإن إزاحة الجسم الذي يتحرك حركة توافقية بسيطة تتغير كدالة جيبية بتغير الزاوية θ كما في الصورة. و بما أن الزاوية θ هي الزاوية التي قطعها الجسم في الزمن (ز) فإن θ =
 ز، و بشكل عام يمكن كتابة معادلة الإزاحة في الحركة التوافقية البسيطة:
ز، و بشكل عام يمكن كتابة معادلة الإزاحة في الحركة التوافقية البسيطة:ص(ز) = صم جا(
 ز + ϕ)
ز + ϕ)حيث، صم: أقصى إزاحة ممكنة للكتلة عن نقطة الإتزان و تساوي نق. ز: الزمن بوحدة الثانية. ϕ: زاوية ثابط الطور، وتحدد موضع الجسم عندما يكون الزمن يساوي صفراً، و تحسب من معرفة موضع الجسم و سرعته عند لحظة معينة.
لاحظ من الصورة "الإزاحة في الحركة التوافقية البسيطة" أن صم تمثل سعة الإهتزاز، و تساوي البعدين نقطة الإتزان و أبعد نقطة ممكنة للحركة، و أن الزمن الدوري (ن) هو الفترة الزمنية التي تفصل بين مرور الجسم في نقطتين متماثلتين في الطور من حيث:
- الموضع.
- اتجاه الحركة.
السرعة في الحركة التوافقية البسيطة
في الصورة "السرعة في الحركة الدائرية" يوجد جسم يتحرك حركة دائرية منتظمة بسرعة مقدارها (ع)، وعندما يكون اتجاه (ع) مماساً للدائرة، أي أن (ع) عمودية على نصف قطر الدائرة، و يمكن حساب مركبة السرعة في الاتجاه السيني:
لاحظ أن جيب الزاوية = جيب تمام الزاوية المتممة
عس = ع جا(
 ز)، و حيث أن ع =
ز)، و حيث أن ع =  نق، فإن:
نق، فإن:عس =
 نق جا(
نق جا( ز)
ز)و لحساب تسارع الجسم في أي لحظة يتم تعويض المعادلة
تس = -
 2 سم جا(
2 سم جا( ز).
ز).الطاقة في الحركة التوافقية البسيطة
عندما يتحرك جسم مربوط بنابض على سطح أملس فإنه يمتلك نوعين من الطاقة:- طاقة حركية، نتيجة سرعته وتعطي بالعلاقة طح = (1 ÷ 2) ك ع2.
- طاقة وضع مخزنة في النابض، نتيجة استطالته و تعطى بالعلاقة طو = (1 ÷ 2) أ س2.
ويسمى مجموع هذين الشكلين من الطاقة بالطاقة الميكانيكية للنظام (طم)؛ أي أن:
طم = طو + طح
طم = (1÷2) أ س2 + (1÷2) ك ع2
وبإهمال قوة الاحتكاك وكتلة النابض يكون مقدار الطاقة الميكانيكية ثابتاً عند جميع النقاط في مسار الجسم.
وفي اللحظة التي يكون فيها الجسم أبعد ما يمكن عن نقطة الاتزان، تكون سرعته تساوي صفراً؛ أي أن:

لاحظ الصورة التي تمثل الطاقة الميكانيكية لكتلة مربوطة في نابض.

